Oblique random forests with `aorsf`

MELODEM data workshop

Author

Affiliation

Byron C. Jaeger, PhD

Wake Forest University School of Medicine

Overview

What does oblique mean?
aorsf
- Motivation
- Design
- Benchmarks
- Applications

What does oblique mean?

Background

Axis-based splits (left) and oblique splits (right)

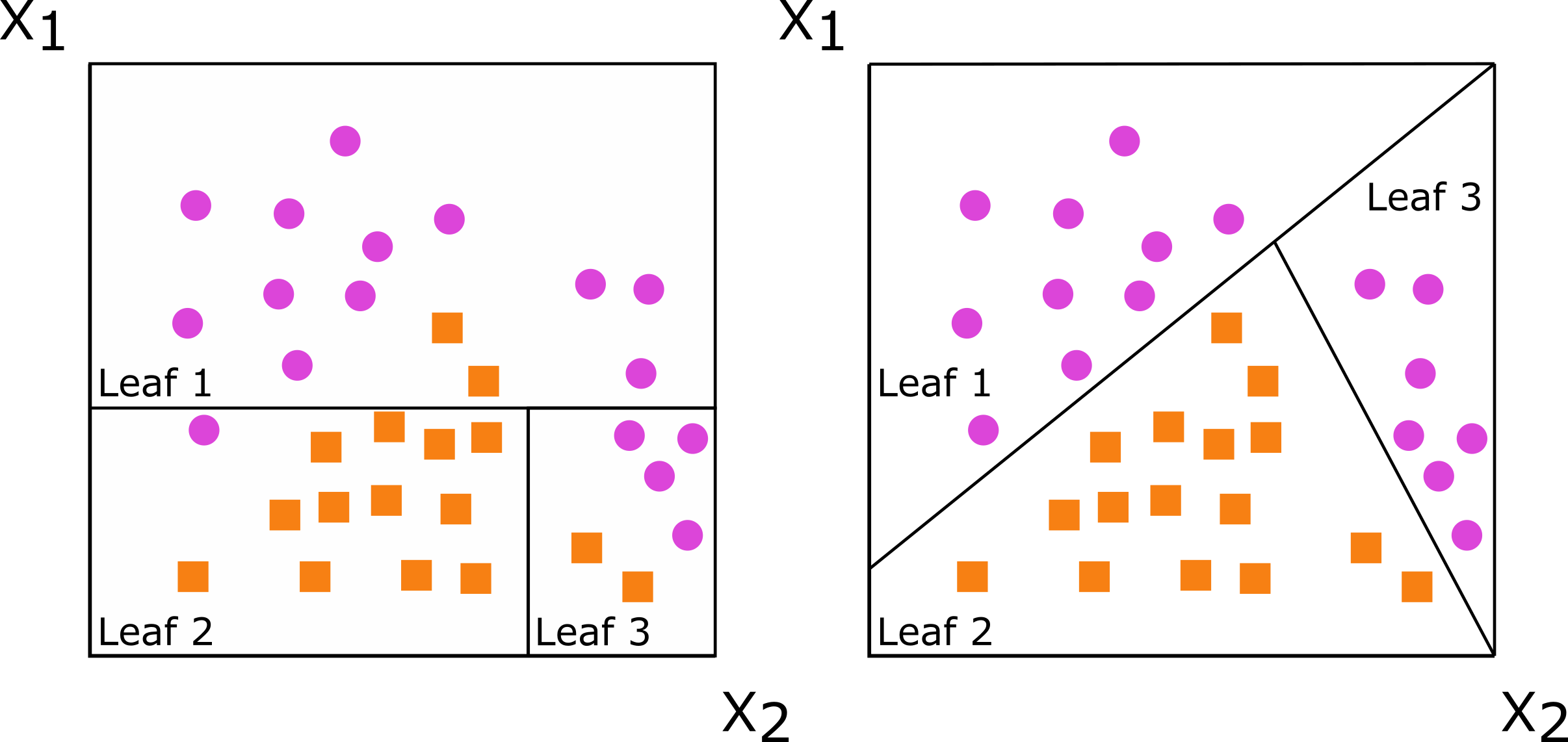
Oblique tree: first split

First, split mostly by bill length

Oblique tree: second split

First, split mostly by bill length

Second, make a triangle for the gentoo.

Oblique random forests

Aggregating randomized trees gives the oblique random forest

Surprisingly different!

Despite very many similarities, axis-based and oblique random forests may give different results.

Prior benchmarks

Breiman (2001) found oblique random forests compared more favorably to boosting than axis based ones.
Menze et al. (2011) coined the term ‘oblique’ random forest and introduced variable importance metrics for it.
On benchmarking 190 classifiers on 121 public datasets, Katuwal, Suganthan, and Zhang (2020) found variations on the oblique random forests were the top 3 classifiers.

Yet, everyone uses axis-based random forests. Few people even know that oblique random forests exist.

Here’s why:

`aorsf`
accelerated oblique random (survival) forest

What is the problem?

Oblique random forests are slow. How slow, you ask?

library(ODRF)
library(ranger)
library(microbenchmark)

microbenchmark(
  ODRF = ODRF(species ~ bill_length_mm + flipper_length_mm, 
              data = penguins, 
              ntrees = 500),
  ranger = ranger(species ~ bill_length_mm + flipper_length_mm,
                  data = penguins,
                  num.trees = 500),
  times = 5
)

Unit: milliseconds
   expr       min        lq      mean    median        uq       max neval cld
   ODRF 4651.9503 4757.0415 4779.5978 4789.0610 4845.8683 4854.0679     5  a 
 ranger   20.2193   20.7901   23.5078   21.8179   23.3712   31.3405     5   b

Why so slow?

Suppose we’re given $p$ continuous predictors, each with $k$ unique values.

If predictor has $k$ unique values $\Rightarrow$ max $k-2$ potential splits
At most, $p \cdot (k-2)$ axis-based splits to assess

Suppose we assess $L$ linear combinations of predictors:

At most, $L \cdot (k-2)$ oblique splits to assess

Usually, $L \gg p$ to find good oblique splits

Find 1 good linear combination?

What if we use a method like regression to find $L=1$ linear combination?

\[\text{Time to assess an oblique split }= R + S\]

Where

$R$ is time to fit regression
$S$ is time to assess up to $k-2$ splits

If $R$ is small, we can do okay with this!

But $R$ is not small

It takes $\approx$ 2.5ms for 1 oblique split, $$20ms to fit 500 axis-based trees…

# compare time for 1 oblique split to 500 axis-based trees
microbenchmark(
  # 1 oblique split
  glm = glm(I(species == 'Adelie') ~ bill_length_mm + flipper_length_mm,
            family = 'binomial', 
            data = penguins),
  # 500 axis based trees
  ranger = ranger(species ~ bill_length_mm + flipper_length_mm,
                  data = penguins,
                  num.trees = 500)
)

Unit: milliseconds
   expr     min       lq      mean   median      uq     max neval cld
    glm  1.7714  2.07825  2.778256  2.47365  2.5821 23.4204   100  a 
 ranger 20.6938 21.58195 21.989103 21.85165 22.0588 40.8994   100   b

1 oblique tree with 10 splits takes longer than 500 axis-based trees 😩

`aorsf`

Jaeger et al. (2022): Accelerated oblique random (survival) forest

We take the approach of minimizing $R$
Instead of fitting a full regression model, we
- Avoid scaling during regression (minimize data copying)
- Relax convergence criteria (e.g., use just 1 iteration)

While model convergence is vital for valid statistical inference, it isn’t that big of a deal for finding oblique splits. Remember, we just have to do slightly better than random guessing.

Benchmark

Minimizing $R$ helps.

microbenchmark(
  ODRF = ODRF(species ~ bill_length_mm + flipper_length_mm, 
              data = penguins, 
              ntrees = 500),
  aorsf = orsf(species ~ bill_length_mm + flipper_length_mm, 
              data = penguins, 
              n_tree = 500),
  ranger = ranger(species ~ bill_length_mm + flipper_length_mm,
                  data = penguins,
                  num.trees = 500),
  times = 5
)

Unit: milliseconds
   expr       min        lq       mean    median        uq       max neval cld
   ODRF 4559.8742 4767.7961 4745.46626 4773.5435 4802.6260 4823.4915     5  a 
  aorsf   46.4154   46.4625   55.92320   51.6300   52.4436   82.6645     5   b
 ranger   21.6600   21.8220   22.42138   22.0821   23.0740   23.4688     5   b

More benchmarks

Jaeger et al. (2024) compare aorsf to obliqueRSF:

Evaluated in 35 risk prediction tasks (21 datasets)
Measured computation time and C-statistic.
Used Bayesian linear mixed models to test for differences.

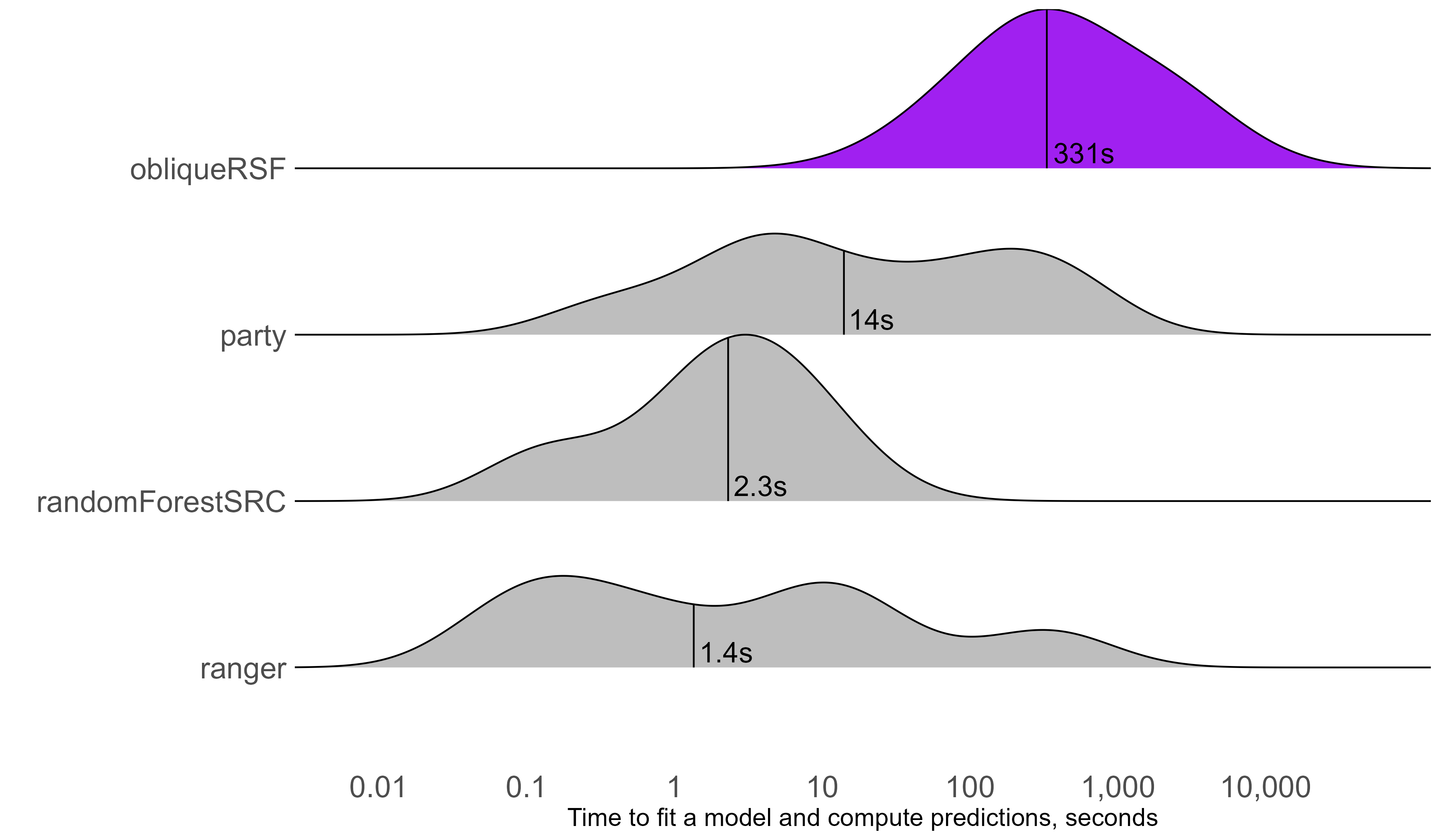
Computation time

aorsf over 300 times faster than obliqueRSF

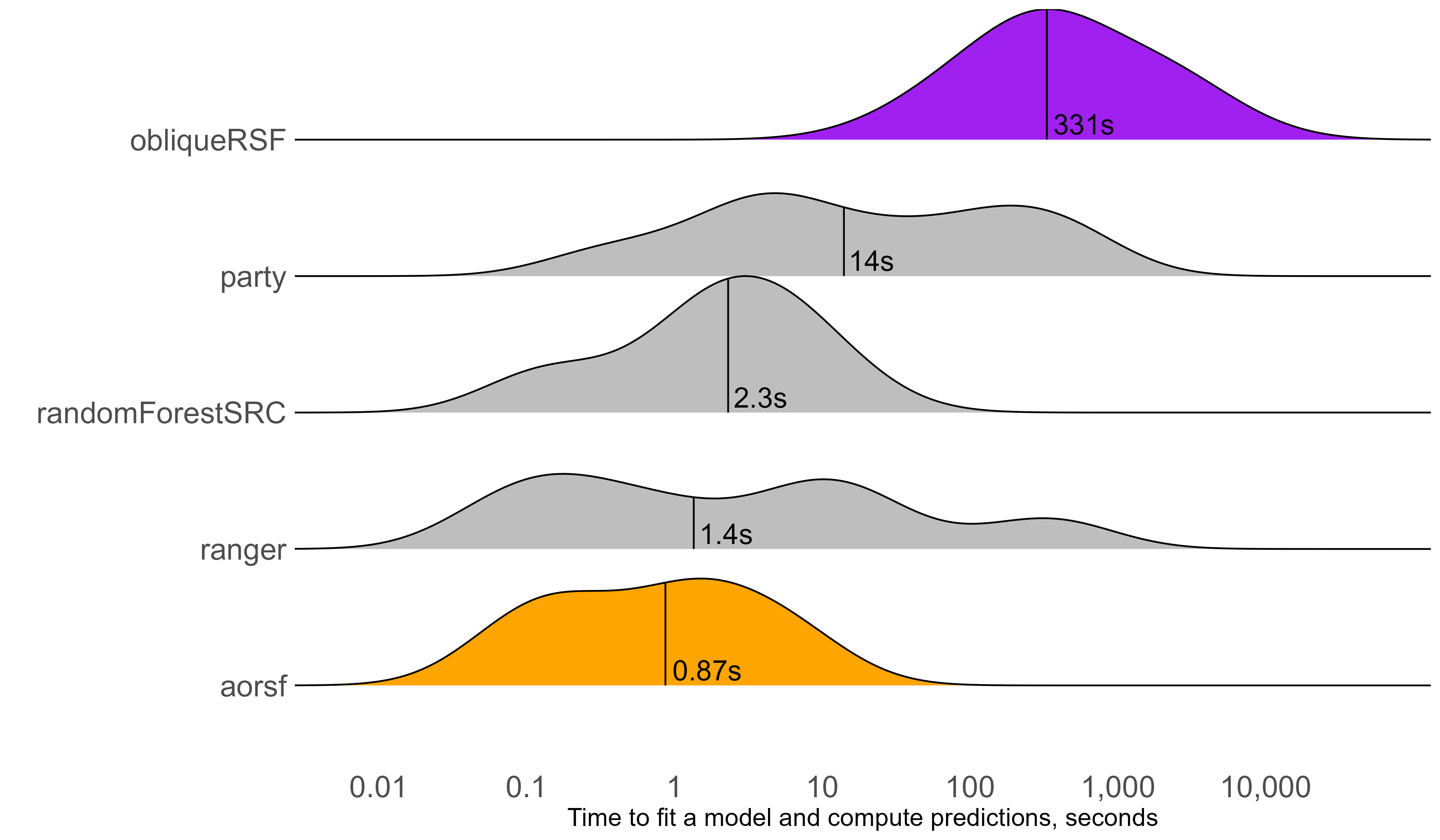
C-statistic

aorsf practically equivalent to obliqueRSF

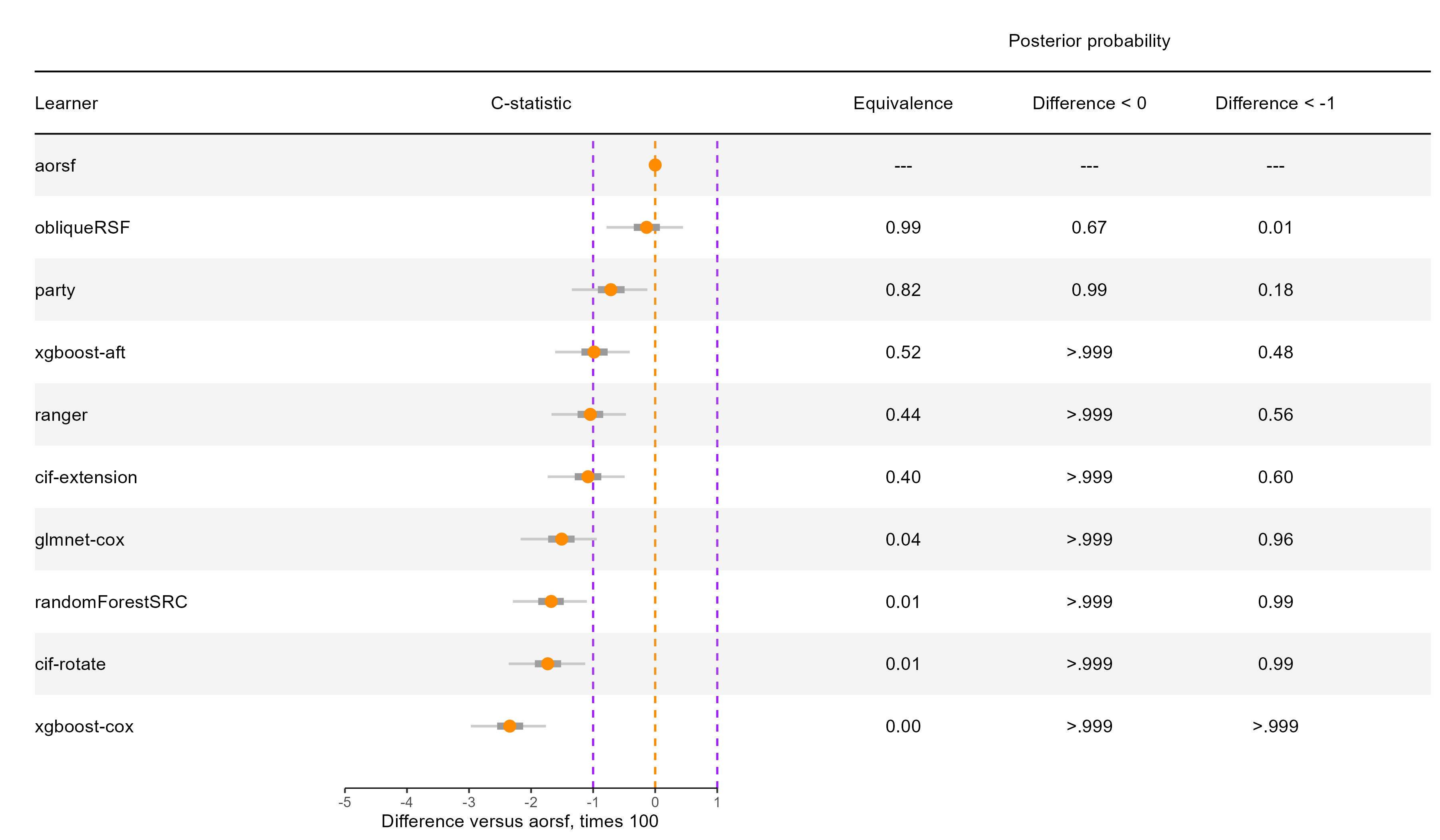
Applications of `aorsf`

Data

I’ll use Alzheimer’s disease data (ad_data) from the modeldata package.

library(modeldata)
glimpse(ad_data, width = 100)

Rows: 333
Columns: 131
$ ACE_CD143_Angiotensin_Converti   <dbl> 2.0031003, 1.5618560, 1.5206598, 1.6808260, 2.4009308, 0.…
$ ACTH_Adrenocorticotropic_Hormon  <dbl> -1.3862944, -1.3862944, -1.7147984, -1.6094379, -0.967584…
$ AXL                              <dbl> 1.09838668, 0.68328157, -0.14527630, 0.68328157, 0.190890…
$ Adiponectin                      <dbl> -5.360193, -5.020686, -5.809143, -5.115996, -4.779524, -5…
$ Alpha_1_Antichymotrypsin         <dbl> 1.7404662, 1.4586150, 1.1939225, 1.2809338, 2.1282317, 1.…
$ Alpha_1_Antitrypsin              <dbl> -12.631361, -11.909882, -13.642963, -15.523564, -11.13306…
$ Alpha_1_Microglobulin            <dbl> -2.577022, -3.244194, -2.882404, -3.170086, -2.343407, -2…
$ Alpha_2_Macroglobulin            <dbl> -72.65029, -154.61228, -136.52918, -98.36175, -144.94460,…
$ Angiopoietin_2_ANG_2             <dbl> 1.06471074, 0.74193734, 0.83290912, 0.91629073, 0.9555114…
$ Angiotensinogen                  <dbl> 2.510547, 2.457283, 1.976365, 2.376085, 2.862219, 2.52402…
$ Apolipoprotein_A_IV              <dbl> -1.427116, -1.660731, -1.660731, -2.120264, -1.171183, -1…
$ Apolipoprotein_A1                <dbl> -7.402052, -7.047017, -7.684284, -8.047190, -6.725434, -7…
$ Apolipoprotein_A2                <dbl> -0.26136476, -0.86750057, -0.65392647, -1.23787436, 0.095…
$ Apolipoprotein_B                 <dbl> -4.624044, -6.747507, -3.976069, -6.517424, -3.378594, -2…
$ Apolipoprotein_CI                <dbl> -1.2729657, -1.2729657, -1.7147984, -1.9661129, -0.755022…
$ Apolipoprotein_CIII              <dbl> -2.312635, -2.343407, -2.748872, -2.995732, -1.514128, -2…
$ Apolipoprotein_D                 <dbl> 2.0794415, 1.3350011, 1.3350011, 1.4350845, 1.6292405, 1.…
$ Apolipoprotein_E                 <dbl> 3.7545215, 3.0971187, 2.7530556, 2.3713615, 3.0671471, 0.…
$ Apolipoprotein_H                 <dbl> -0.15734908, -0.57539617, -0.34483937, -0.53172814, 0.662…
$ B_Lymphocyte_Chemoattractant_BL  <dbl> 2.2969819, 1.6731213, 1.6731213, 1.9805094, 2.2969819, 2.…
$ BMP_6                            <dbl> -2.200744, -1.728053, -2.062421, -1.982912, -1.241520, -1…
$ Beta_2_Microglobulin             <dbl> 0.69314718, 0.47000363, 0.33647224, 0.64185389, 0.3364722…
$ Betacellulin                     <int> 34, 53, 49, 52, 67, 51, 41, 42, 58, 59, 32, 43, 51, 53, 4…
$ C_Reactive_Protein               <dbl> -4.074542, -6.645391, -8.047190, -6.214608, -4.342806, -7…
$ CD40                             <dbl> -0.7964147, -1.2733760, -1.2415199, -1.1238408, -0.924034…
$ CD5L                             <dbl> 0.09531018, -0.67334455, 0.09531018, -0.32850407, 0.36331…
$ Calbindin                        <dbl> 33.21363, 25.27636, 22.16609, 23.45584, 21.83275, 13.2315…
$ Calcitonin                       <dbl> 1.3862944, 3.6109179, 2.1162555, -0.1508229, 1.3083328, 1…
$ CgA                              <dbl> 397.6536, 465.6759, 347.8639, 334.2346, 442.8046, 137.947…
$ Clusterin_Apo_J                  <dbl> 3.555348, 3.044522, 2.772589, 2.833213, 3.044522, 2.56494…
$ Complement_3                     <dbl> -10.36305, -16.10824, -16.10824, -13.20556, -12.81314, -1…
$ Complement_Factor_H              <dbl> 3.5737252, 3.6000471, 4.4745686, 3.0971187, 7.2451496, 3.…
$ Connective_Tissue_Growth_Factor  <dbl> 0.5306283, 0.5877867, 0.6418539, 0.5306283, 0.9162907, 0.…
$ Cortisol                         <dbl> 10.0, 12.0, 10.0, 14.0, 11.0, 13.0, 4.9, 13.0, 12.0, 17.0…
$ Creatine_Kinase_MB               <dbl> -1.710172, -1.751002, -1.383559, -1.647864, -1.625834, -1…
$ Cystatin_C                       <dbl> 9.041922, 9.067624, 8.954157, 9.581904, 8.977146, 7.83597…
$ EGF_R                            <dbl> -0.1354543, -0.3700474, -0.7329871, -0.4218532, -0.620603…
$ EN_RAGE                          <dbl> -3.688879, -3.816713, -4.755993, -2.937463, -2.364460, -3…
$ ENA_78                           <dbl> -1.349543, -1.356595, -1.390672, -1.367775, -1.339440, -1…
$ Eotaxin_3                        <int> 53, 62, 62, 44, 64, 57, 64, 64, 64, 70, 82, 73, 70, 67, 3…
$ FAS                              <dbl> -0.08338161, -0.52763274, -0.63487827, -0.47803580, -0.12…
$ FSH_Follicle_Stimulation_Hormon  <dbl> -0.6516715, -1.6272839, -1.5630004, -0.5902871, -0.976300…
$ Fas_Ligand                       <dbl> 3.1014922, 2.9788133, 1.3600098, 2.5372201, 4.0372847, 2.…
$ Fatty_Acid_Binding_Protein       <dbl> 2.5208712, 2.2477966, 0.9063009, 0.6237306, 2.6345883, 0.…
$ Ferritin                         <dbl> 3.329165, 3.932959, 3.176872, 3.138093, 2.690416, 1.84707…
$ Fetuin_A                         <dbl> 1.2809338, 1.1939225, 1.4109870, 0.7419373, 2.1517622, 1.…
$ Fibrinogen                       <dbl> -7.035589, -8.047190, -7.195437, -7.799353, -6.980326, -6…
$ GRO_alpha                        <dbl> 1.381830, 1.372438, 1.412679, 1.372438, 1.398431, 1.39843…
$ Gamma_Interferon_induced_Monokin <dbl> 2.949822, 2.721793, 2.762231, 2.885476, 2.851987, 2.82244…
$ Glutathione_S_Transferase_alpha  <dbl> 1.0641271, 0.8670202, 0.8890150, 0.7083677, 1.2358607, 1.…
$ HB_EGF                           <dbl> 6.559746, 8.754531, 7.745463, 5.949436, 7.245150, 6.41301…
$ HCC_4                            <dbl> -3.036554, -4.074542, -3.649659, -3.816713, -3.146555, -3…
$ Hepatocyte_Growth_Factor_HGF     <dbl> 0.58778666, 0.53062825, 0.09531018, 0.40546511, 0.5306282…
$ I_309                            <dbl> 3.433987, 3.135494, 2.397895, 3.367296, 3.761200, 2.70805…
$ ICAM_1                           <dbl> -0.1907787, -0.4620172, -0.4620172, -0.8572661, 0.0971503…
$ IGF_BP_2                         <dbl> 5.609472, 5.347108, 5.181784, 5.424950, 5.420535, 5.05624…
$ IL_11                            <dbl> 5.121987, 4.936704, 4.665910, 6.223931, 7.070709, 6.10321…
$ IL_13                            <dbl> 1.282549, 1.269463, 1.274133, 1.307549, 1.309980, 1.28254…
$ IL_16                            <dbl> 4.192081, 2.876338, 2.616102, 2.441056, 4.736472, 2.67103…
$ IL_17E                           <dbl> 5.731246, 6.705891, 4.149327, 4.695848, 4.204987, 3.63705…
$ IL_1alpha                        <dbl> -6.571283, -8.047190, -8.180721, -7.600902, -6.943657, -8…
$ IL_3                             <dbl> -3.244194, -3.912023, -4.645992, -4.268698, -2.995732, -3…
$ IL_4                             <dbl> 2.484907, 2.397895, 1.824549, 1.481605, 2.708050, 1.20896…
$ IL_5                             <dbl> 1.09861229, 0.69314718, -0.24846136, 0.78845736, 1.163150…
$ IL_6                             <dbl> 0.26936976, 0.09622438, 0.18568645, -0.37116408, -0.07204…
$ IL_6_Receptor                    <dbl> 0.64279595, 0.43115645, 0.09668586, 0.57519641, 0.0966858…
$ IL_7                             <dbl> 4.8050453, 3.7055056, 1.0056222, 2.3362105, 4.2875620, 2.…
$ IL_8                             <dbl> 1.711325, 1.675557, 1.691393, 1.719944, 1.764298, 1.70827…
$ IP_10_Inducible_Protein_10       <dbl> 6.242223, 5.686975, 5.049856, 5.602119, 6.369901, 5.48063…
$ IgA                              <dbl> -6.812445, -6.377127, -6.319969, -7.621105, -4.645992, -5…
$ Insulin                          <dbl> -0.6258253, -0.9431406, -1.4466191, -1.4852687, -0.300311…
$ Kidney_Injury_Molecule_1_KIM_1   <dbl> -1.204295, -1.197703, -1.191191, -1.231557, -1.163800, -1…
$ LOX_1                            <dbl> 1.7047481, 1.5260563, 1.1631508, 1.2237754, 1.3609766, 0.…
$ Leptin                           <dbl> -1.5290628, -1.4660558, -1.6622675, -1.2693924, -0.915106…
$ Lipoprotein_a                    <dbl> -4.268698, -4.933674, -5.843045, -4.990833, -2.937463, -4…
$ MCP_1                            <dbl> 6.740519, 6.849066, 6.767343, 6.781058, 6.722630, 6.54103…
$ MCP_2                            <dbl> 1.9805094, 1.8088944, 0.4005958, 1.9805094, 2.2208309, 2.…
$ MIF                              <dbl> -1.237874, -1.897120, -2.302585, -1.660731, -1.897120, -2…
$ MIP_1alpha                       <dbl> 4.968453, 3.690160, 4.049508, 4.928562, 6.452764, 4.60342…
$ MIP_1beta                        <dbl> 3.258097, 3.135494, 2.397895, 3.218876, 3.526361, 2.89037…
$ MMP_2                            <dbl> 4.478566, 3.781473, 2.866631, 2.968511, 3.690160, 2.91776…
$ MMP_3                            <dbl> -2.207275, -2.465104, -2.302585, -1.771957, -1.560648, -3…
$ MMP10                            <dbl> -3.270169, -3.649659, -2.733368, -4.074542, -2.617296, -3…
$ MMP7                             <dbl> -3.7735027, -5.9681907, -4.0302269, -6.8561489, -0.222222…
$ Myoglobin                        <dbl> -1.89711998, -0.75502258, -1.38629436, -1.13943428, -1.77…
$ NT_proBNP                        <dbl> 4.553877, 4.219508, 4.248495, 4.110874, 4.465908, 4.18965…
$ NrCAM                            <dbl> 5.003946, 5.209486, 4.744932, 4.969813, 5.198497, 3.25809…
$ Osteopontin                      <dbl> 5.356586, 6.003887, 5.017280, 5.768321, 5.693732, 4.73619…
$ PAI_1                            <dbl> 1.00350156, -0.03059880, 0.43837211, 0.00000000, 0.252304…
$ PAPP_A                           <dbl> -2.902226, -2.813276, -2.935541, -2.786601, -2.935541, -2…
$ PLGF                             <dbl> 4.442651, 4.025352, 4.510860, 3.433987, 4.795791, 4.39444…
$ PYY                              <dbl> 3.218876, 3.135494, 2.890372, 2.833213, 3.663562, 3.33220…
$ Pancreatic_polypeptide           <dbl> 0.57878085, 0.33647224, -0.89159812, -0.82098055, 0.26236…
$ Prolactin                        <dbl> 0.00000000, -0.51082562, -0.13926207, -0.04082199, 0.1823…
$ Prostatic_Acid_Phosphatase       <dbl> -1.620527, -1.739232, -1.636682, -1.739232, -1.696685, -1…
$ Protein_S                        <dbl> -1.784998, -2.463991, -2.259135, -2.703458, -1.659842, -2…
$ Pulmonary_and_Activation_Regulat <dbl> -0.8439701, -2.3025851, -1.6607312, -1.1086626, -0.562118…
$ RANTES                           <dbl> -6.214608, -6.938214, -6.645391, -5.991465, -6.319969, -6…
$ Resistin                         <dbl> -16.475315, -16.025283, -16.475315, -13.501240, -11.09283…
$ S100b                            <dbl> 1.5618560, 1.7566212, 1.4357282, 1.2543998, 1.3012972, 1.…
$ SGOT                             <dbl> -0.94160854, -0.65392647, 0.33647224, -0.19845094, 0.0953…
$ SHBG                             <dbl> -1.897120, -1.560648, -2.207275, -3.146555, -2.430418, -2…
$ SOD                              <dbl> 5.609472, 5.814131, 5.723585, 5.771441, 5.655992, 4.54329…
$ Serum_Amyloid_P                  <dbl> -5.599422, -6.119298, -5.381699, -6.645391, -5.203007, -5…
$ Sortilin                         <dbl> 4.908629, 5.478731, 3.810182, 3.402176, 3.402176, 2.97881…
$ Stem_Cell_Factor                 <dbl> 4.174387, 3.713572, 3.433987, 3.951244, 4.060443, 2.56494…
$ TGF_alpha                        <dbl> 8.649098, 11.331619, 10.858497, 9.454406, 8.323453, 10.00…
$ TIMP_1                           <dbl> 15.204651, 11.266499, 12.282857, 11.114877, 13.748016, 11…
$ TNF_RII                          <dbl> -0.06187540, -0.32850407, -0.41551544, -0.34249031, -0.34…
$ TRAIL_R3                         <dbl> -0.1829004, -0.5007471, -0.9240345, -0.3848591, -0.858259…
$ TTR_prealbumin                   <dbl> 2.944439, 2.833213, 2.944439, 2.944439, 3.044522, 3.04452…
$ Tamm_Horsfall_Protein_THP        <dbl> -3.095810, -3.111190, -3.166721, -3.155652, -3.038017, -3…
$ Thrombomodulin                   <dbl> -1.340566, -1.675252, -1.534276, -1.975407, -1.210709, -1…
$ Thrombopoietin                   <dbl> -0.1026334, -0.6733501, -0.9229670, -0.7510004, 0.0976177…
$ Thymus_Expressed_Chemokine_TECK  <dbl> 4.149327, 3.810182, 2.791992, 4.037285, 4.534163, 4.53416…
$ Thyroid_Stimulating_Hormone      <dbl> -3.863233, -4.828314, -4.990833, -4.892852, -4.645992, -4…
$ Thyroxine_Binding_Globulin       <dbl> -1.4271164, -1.6094379, -1.8971200, -2.0402208, -0.478035…
$ Tissue_Factor                    <dbl> 2.04122033, 2.02814825, 1.43508453, 2.02814825, 1.9878743…
$ Transferrin                      <dbl> 3.332205, 2.890372, 2.890372, 2.890372, 3.496508, 2.99573…
$ Trefoil_Factor_3_TFF3            <dbl> -3.381395, -3.912023, -3.729701, -3.816713, -3.442019, -4…
$ VCAM_1                           <dbl> 3.258097, 2.708050, 2.639057, 2.772589, 3.044522, 2.20827…
$ VEGF                             <dbl> 22.03456, 18.60184, 17.47619, 17.54560, 20.77860, 13.1976…
$ Vitronectin                      <dbl> -0.04082199, -0.38566248, -0.22314355, -0.65392647, 0.166…
$ von_Willebrand_Factor            <dbl> -3.146555, -3.863233, -3.540459, -3.863233, -3.816713, -4…
$ age                              <dbl> 0.9876238, 0.9861496, 0.9866667, 0.9867021, 0.9871630, 0.…
$ tau                              <dbl> 6.297754, 6.659294, 6.270988, 6.152733, 6.623707, 5.36129…
$ p_tau                            <dbl> 4.348108, 4.859967, 4.400247, 4.494886, 4.524589, 3.46573…
$ Ab_42                            <dbl> 12.019678, 11.015759, 12.302271, 12.398138, 11.024109, 11…
$ male                             <dbl> 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, …
$ Genotype                         <fct> E3E3, E3E4, E3E4, E3E4, E3E3, E4E4, E2E3, E2E3, E3E3, E2E…
$ Class                            <fct> Control, Control, Control, Control, Control, Impaired, Co…

Model fitting

Formula interface

Similar to other R packages
Shortcut: outcome ~ .

library(aorsf)
fit <- orsf(ad_data, Class ~ .)

---------- Oblique random classification forest

     Linear combinations: Accelerated Logistic regression
          N observations: 333
               N classes: 2
                 N trees: 500
      N predictors total: 130
   N predictors per node: 12
 Average leaves per tree: 13.122
Min observations in leaf: 5
          OOB stat value: 0.88
           OOB stat type: AUC-ROC
     Variable importance: anova

-----------------------------------------

Your turn

Open classwork/03-oblique_forests.qmd and complete Exercise 1

05:00

Random splits

Compare ‘random splits’ to the accelerated regression approach.

Create random linear combinations

f_rando <- function(x_node, y_node, w_node){
  matrix(runif(ncol(x_node)), ncol=1) 
}

control_rando <- orsf_control_classification(f_rando)

Keep making them until a split is found that is ‘good enough’

fit_rando = orsf(ad_data, formula = Class ~ ., 
                 tree_seeds = 1, 
                 n_retry = 100,
                 split_rule = 'cstat', 
                 split_min_stat = .6,
                 control = control_rando)

Compare computational efficiency

‘Many splits’ is slower

microbenchmark::microbenchmark(
  rando = orsf(ad_data, formula = Class ~ ., 
               tree_seeds = 1, n_retry = 500,
               split_rule = 'cstat', split_min_stat = .6,
               control = control_rando),
  accel = orsf(ad_data, formula = Class ~ ., 
               tree_seeds = 1, split_rule = 'cstat',
               split_min_stat = .6),
  times = 5
)

Unit: milliseconds
  expr       min        lq      mean   median       uq       max neval cld
 rando 1103.7639 1111.5100 1173.4211 1133.069 1135.577 1383.1855     5  a 
 accel  101.4826  109.4326  115.1902  115.645  119.620  129.7707     5   b

Compare out-of-bag prediction accuracy

Out-of-bag C-statistic for random splits:

fit_rando$eval_oobag$stat_values

          [,1]
[1,] 0.7875307

Out-of-bag C-statistic for accelerated regression:

fit_accel$eval_oobag$stat_values

          [,1]
[1,] 0.8968304

$\Rightarrow$ accelerated regression is faster and more accurate

Partial dependence

Purpose: Interpret a model.

Description: Expected prediction from a model as a function of a single predictor or multiple predictors. The expectation is marginalized over the values of all other predictors, giving something like a multivariable adjusted estimate of the model’s prediction.

Example: Expected 10-year mortality risk as a function of age.

Pseudo-code:

for i in seq(min_age, max_age){
  
 - Set all values of age to i in the training data
 - Compute out-of-bag predictions for training data
 - Save the mean prediction and i
  
}

Single variable summary

Similar to summary(), orsf_summarize_uni() computes out-of-bag partial dependence on the number of variables you request.

orsf_summarize_uni(fit, n_variables = 1, class = "Impaired")


-- tau (VI Rank: 1) ----------------------------

        |------------ Probability ------------|
  Value      Mean    Median    25th %    75th %
 <char>     <num>     <num>     <num>     <num>
   5.04 0.2322465 0.1929924 0.1187406 0.3173001
   5.37 0.2369582 0.1963388 0.1223932 0.3234504
   5.75 0.2529760 0.2109251 0.1293360 0.3498093
   6.18 0.2817313 0.2352786 0.1531655 0.3805347
   6.50 0.3011033 0.2557926 0.1721181 0.4076272

 Predicted probability for top 1 predictors

Multi-variable summary

See if predictors interact (they don’t in this case)

pd <- orsf_pd_oob(fit, pred_spec_auto(tau, Genotype))

Your turn

Complete exercise 2

05:00

Variable selection

We want to remove predictors that don’t have any prognostic value.

orsf_vs() performs recursive feature elimination.
Fit a forest and estimate importance
Drop the least important predictor
Repeat until < n_predictor_min predictors left.

orsf_vars <- orsf_vs(fit, 
                     n_predictor_min = 1, 
                     verbose_progress = TRUE)

Selecting variables: 34.9% ~ time remaining: 6 seconds 
Selecting variables: 81.4% ~ time remaining: 1 seconds 
Selecting variables: 100%

Faster

If needed, reduce n_tree and increase leaf_min_obs to speed this up

fit_light <- orsf_update(fit, n_tree = 100, leaf_min_obs = 20)

orsf_vars_light <- orsf_vs(fit_light, n_predictor_min = 1, verbose_progress = TRUE)

Selecting variables: 100%

Pick your variables

Plot the history of performance and variables included.

max_auc <- orsf_vars %>% 
  arrange(desc(stat_value)) %>% 
  slice(1)

fig <- ggplot(orsf_vars) + 
  aes(x = n_predictors,
      y = stat_value) + 
  geom_point(alpha = 0.5) + 
  geom_smooth(se = FALSE, 
              linewidth = 1) + 
  geom_point(data = max_auc, 
             size = 3, 
             color = 'purple')

Your turn

Complete exercise 3

05:00

Compare models

For causal random forests, we’ll need good prediction models for both dementia and APOE4 status.

Developing and evaluating prediction models is a deep topic.
We will cover the basics:
- Data splitting
- Pre-processing
- Evaluating in test data

We’ll do this using the tidymodels framework.

Data splitting

If you evaluate prediction models with their training data, you

Reward models that overfit the data.
Don’t learn much about what will happen in the real world.

So, always evaluate prediction models with data that is “new”

library(rsample)
set.seed(1234)
# make the split: 50% training data, 50% testing
split <- initial_split(data = ad_data, prop = 1/2)
# get the training data
train <- training(split)
# get the testing data
test <- testing(split)

Pre-processing

Why do we pre-process data?

Some models require special data format
Impute missing values correctly
Sometimes its helpful to apply transformations to data prior to modeling

We’ll train our pre-processing steps using the recipes package

library(recipes)

# Makes the recipe steps
recipe_steps <- recipe(data = train, Class ~ .) %>% 
  step_impute_knn(all_predictors()) %>% 
  step_dummy(all_nominal_predictors())

Training the recipe

With its steps defined, we are ready to

train the recipe

# train the recipe steps with training data
recipe_trained <- prep(recipe_steps, training = train)

use it to process the training and testing data.

# apply the recipe steps to process training data
train_processed <- bake(recipe_trained, new_data = train)
# apply the exact same steps to the testing data
test_processed <- bake(recipe_trained, new_data = test)

Fitting models

parsnip is a unified interface for models with R.
bonsai extends parsnip, focusing on decision tree models.

With these packages, we make a model specification, and then fit it.

library(parsnip)
library(bonsai)

# make model specifications
ranger_spec <- rand_forest(mode = 'classification', engine = 'ranger')
aorsf_spec  <- rand_forest(mode = 'classification', engine = 'aorsf')

# fit them
ranger_fit <- fit(ranger_spec, data = train_processed, formula = Class ~ .)
aorsf_fit  <- fit(aorsf_spec,  data = train_processed, formula = Class ~ .)

Evaluating in test data

We predict probabilities for observations in the testing data, and evaluate discrimination using the yardstick package:

preds <- list(aorsf = aorsf_fit, ranger = ranger_fit) %>% 
  map(~ predict(.x, new_data = test_processed, type = 'prob')) %>% 
  map(~ mutate(.x, truth = test_processed$Class)) %>% 
  bind_rows(.id = 'model')

library(yardstick)

preds %>% 
  group_by(model) %>% 
  roc_auc(truth = truth, .pred_Impaired)

# A tibble: 3 × 4
  model  .metric .estimator .estimate
  <chr>  <chr>   <chr>          <dbl>
1 aorsf  roc_auc binary         0.936
2 odrf   roc_auc binary         0.940
3 ranger roc_auc binary         0.918

To the pipeline

Copy/paste this code into your _targets.R file.

# in _targets.R, you should see this comment: 

# real data model targets (to be added as an exercise). 

# Paste this code right beneath that.

fit_aorsf_zzzz_tar <- tar_target(
  fit_aorsf_zzzz,
  fit_orsf_clsf(data = data_zzzz)
)

Modify this code, replacing zzzz with the name of your dataset.

References

Breiman, Leo. 2001. “Random Forests.” Machine Learning 45: 5–32.

Jaeger, Byron C, Sawyer Welden, Kristin Lenoir, and Nicholas M Pajewski. 2022. “Aorsf: An r Package for Supervised Learning Using the Oblique Random Survival Forest.” Journal of Open Source Software 7 (77): 4705.

Jaeger, Byron C, Sawyer Welden, Kristin Lenoir, Jaime L Speiser, Matthew W Segar, Ambarish Pandey, and Nicholas M Pajewski. 2024. “Accelerated and Interpretable Oblique Random Survival Forests.” Journal of Computational and Graphical Statistics 33 (1): 192–207.

Katuwal, Rakesh, Ponnuthurai Nagaratnam Suganthan, and Le Zhang. 2020. “Heterogeneous Oblique Random Forest.” Pattern Recognition 99: 107078.

Menze, Bjoern H, B Michael Kelm, Daniel N Splitthoff, Ullrich Koethe, and Fred A Hamprecht. 2011. “On Oblique Random Forests.” In Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2011, Athens, Greece, September 5-9, 2011, Proceedings, Part II 22, 453–69. Springer.

Other Formats

Overview

What does oblique mean?

Background

Oblique tree: first split

Oblique tree: second split

Oblique random forests

Surprisingly different!

Prior benchmarks

Here’s why:

aorsf accelerated oblique random (survival) forest

What is the problem?

Why so slow?

Find 1 good linear combination?

But \(R\) is not small

aorsf

Benchmark

More benchmarks

Computation time

C-statistic

Applications of aorsf

Data

Data

Model fitting

Your turn

Random splits

Compare computational efficiency

Compare out-of-bag prediction accuracy

Partial dependence

Single variable summary

Multi-variable summary

Your turn

Variable selection

Faster

Pick your variables

Your turn

Compare models

Data splitting

Pre-processing

Training the recipe

Fitting models

Evaluating in test data

To the pipeline

References

`aorsf`
accelerated oblique random (survival) forest

`aorsf`

Applications of `aorsf`