Resampling with scalib objects

library(survival.calib)
library(survival)
library(riskRegression)
#> riskRegression version 2022.03.22
library(dplyr)
#> 
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union
library(tidyr)
library(ggplot2)
library(data.table)
#> 
#> Attaching package: 'data.table'
#> The following objects are masked from 'package:dplyr':
#> 
#>     between, first, last

theme_set(theme_bw() + theme(panel.grid = element_blank()))

knitr::opts_chunk$set(fig.width=7, fig.height=5)

Data

For this example, we’ll use a standard dataset, survival::flchain, with some modifications:

1. we omit cases with missing values

   # drop rows with missing values for simplicity
   data_init <- na.omit(flchain)

2. we remove the chapter variable.

   # sometimes chapter makes split-sample tests tricky
   data_init$chapter <- NULL

   Leaving us with a pretty clean initial data set

head(data_init)
#>   age sex sample.yr kappa lambda flc.grp creatinine mgus futime death
#> 1  97   F      1997  5.70  4.860      10        1.7    0     85     1
#> 2  92   F      2000  0.87  0.683       1        0.9    0   1281     1
#> 3  94   F      1997  4.36  3.850      10        1.4    0     69     1
#> 4  92   F      1996  2.42  2.220       9        1.0    0    115     1
#> 5  93   F      1996  1.32  1.690       6        1.1    0   1039     1
#> 6  90   F      1997  2.01  1.860       9        1.0    0   1355     1

Repeated split sample tests

set.seed(7302016)

mccv_count <- 10

results <- vector(mode = 'list', length = mccv_count)

n_obs_total <- nrow(data_init)
n_obs_train <- round(n_obs_total * 1/2)
pred_horizon <- 1500

for(i in seq(mccv_count)){

  train_index <- sample(n_obs_total, size = n_obs_train)
  data_train <- data_init[train_index, ]
  data_test <- data_init[-train_index, ]

  model <- coxph(Surv(futime, death) ~ age + sex + sample.yr + flc.grp,
               data = data_train,
               x = TRUE)

  predrisk <- predictRisk(model, newdata = data_test, times = pred_horizon)

  results[[i]] <- predrisk %>% 
  scalib(pred_horizon = pred_horizon,
         event_status = data_test$death,
         event_time = data_test$futime) %>% 
  scalib_hare() %>% 
  scalib_gnd() %>% 
  as.data.table()

}

results <- rbindlist(results, idcol = '._iter_.')

results
#>     ._iter_.      ._id_. pred_horizon              inputs            outputs
#>  1:        1 pred_risk_1         1500 <data.table[981x3]> <data.table[1x11]>
#>  2:        2 pred_risk_1         1500 <data.table[981x3]> <data.table[1x11]>
#>  3:        3 pred_risk_1         1500 <data.table[981x3]> <data.table[1x11]>
#>  4:        4 pred_risk_1         1500 <data.table[981x3]> <data.table[1x11]>
#>  5:        5 pred_risk_1         1500 <data.table[981x3]> <data.table[1x11]>
#>  6:        6 pred_risk_1         1500 <data.table[981x3]> <data.table[1x11]>
#>  7:        7 pred_risk_1         1500 <data.table[981x3]> <data.table[1x11]>
#>  8:        8 pred_risk_1         1500 <data.table[981x3]> <data.table[1x11]>
#>  9:        9 pred_risk_1         1500 <data.table[981x3]> <data.table[1x11]>
#> 10:       10 pred_risk_1         1500 <data.table[981x3]> <data.table[1x11]>

Extracting outputs

data_outputs <- results  %>% 
  select(._iter_., ._id_., outputs) %>% 
  unnest(outputs)

Pooling Chi-square statistics for miscalibration

Don’t do this! The assumption of pooled chi-square tests is that the chi-square statistics are independent, but these chi-square statistics are correlated.

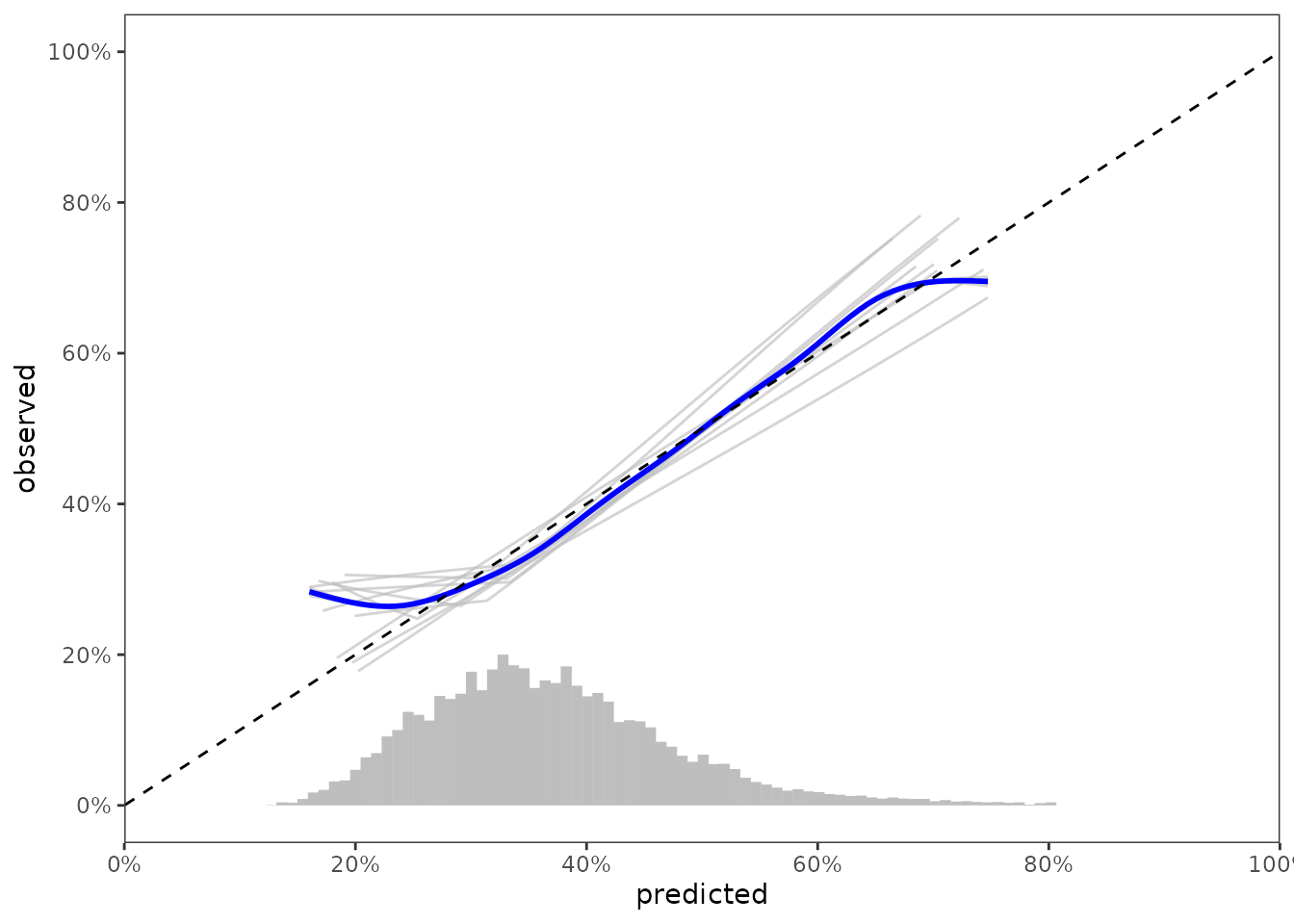
Visualizing results across all resamples

data_segment <- results %>% 
  select(._id_., inputs) %>% 
  unnest(inputs) %>% 
  pull(pred_risk) %>% 
  predrisk_bin_segments(bin_count = 75,
                        bin_length = 2)


data_calslope <- data_outputs %>% 
  select(._iter_., ._id_., hare_data_plot) %>% 
  unnest(hare_data_plot)


ggplot(data_calslope) +
  aes(x = predicted, y = observed, group = ._iter_.) +
  geom_line(col = 'grey', alpha = 2/3) +
  geom_smooth(col = 'blue', 
              group = 1, 
              method = 'gam',
              formula = y ~ s(x, bs = "cs")) +
  geom_abline(col = 'black', linetype = 2, intercept = 0, slope = 1) +
  scale_x_continuous(limits = c(0, 1),
                     expand = c(0, 0),
                     breaks = seq(0, 1, by = 0.2),
                     labels = paste0(seq(0, 100, by = 20),"%")) +
  scale_y_continuous(limits = c(0, 1),
                     breaks = seq(0, 1, by = 0.2),
                     labels = paste0(seq(0, 100, by = 20),"%")) +
  labs(color = 'Event status\nat t = 1,000') +
  geom_segment(data = data_segment,
               inherit.aes = FALSE,
               size = 2,
               color = 'grey',
               mapping = aes(x = x,
                             y = y,
                             xend = xend,
                             yend = yend))